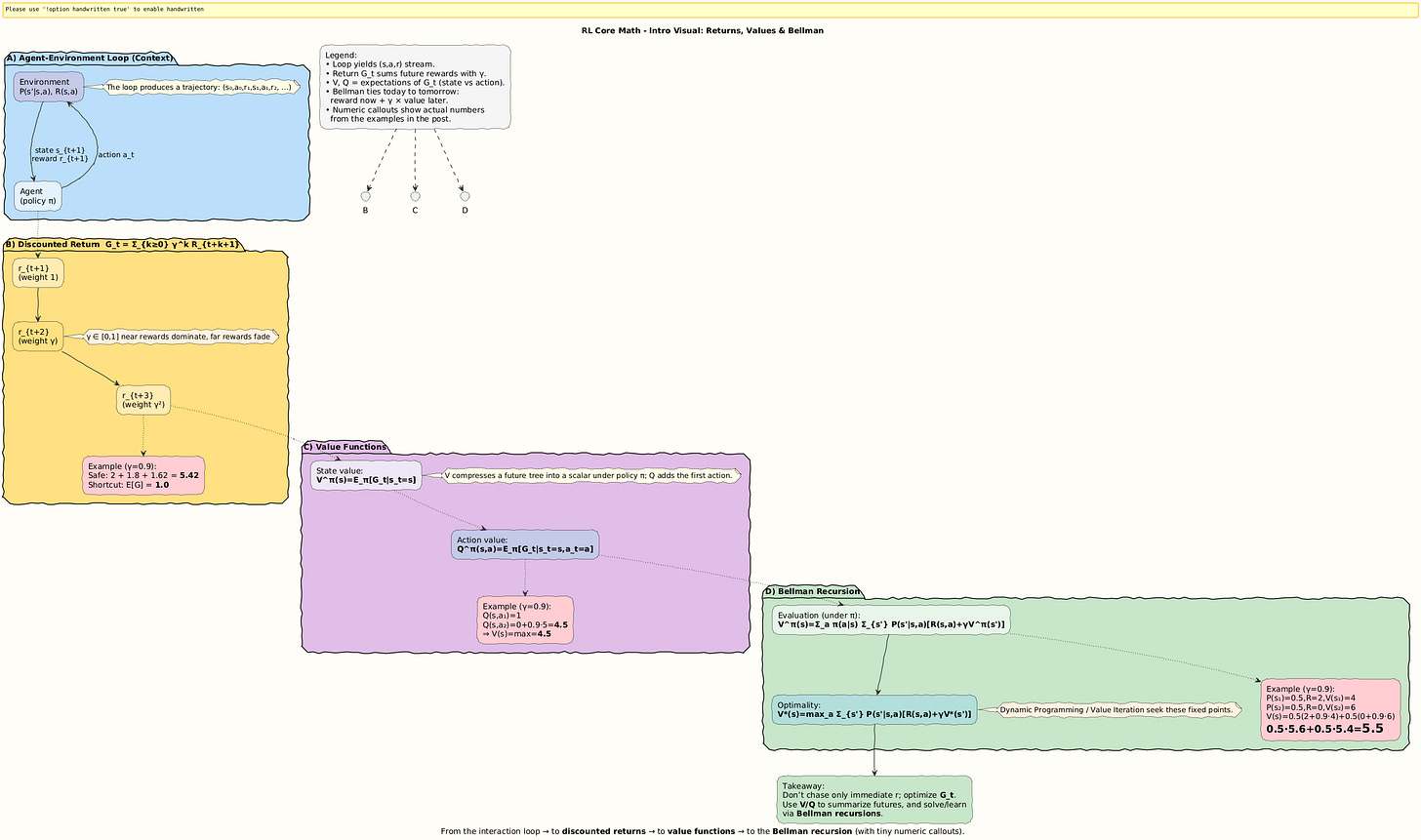
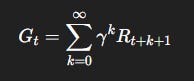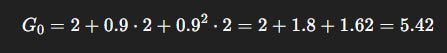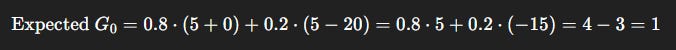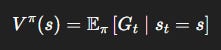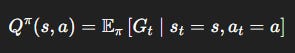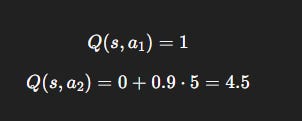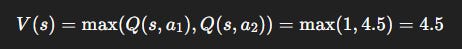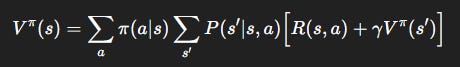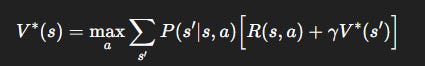The Core Math of Reinforcement Learning: Returns, Values, and the Bellman Equation
Setting the Scene: Why Do Agents Look Ahead?
Imagine a child playing Mario. If they only cared about this second, they’d grab the nearest coin and maybe fall into a pit right after. But if they cared about the long-term, they’d plan: jump carefully, avoid enemies, and maybe win the level.
That’s what Reinforcement Learning (RL) formalizes: the balance between short-term gratification and long-term planning.
The math of RL revolves around three intertwined ideas:
Returns: adding up rewards into the future.
Value Functions: predicting how good states or actions are.
The Bellman Equation: a recursion that forces agents to think forward.
Let’s go step by step.
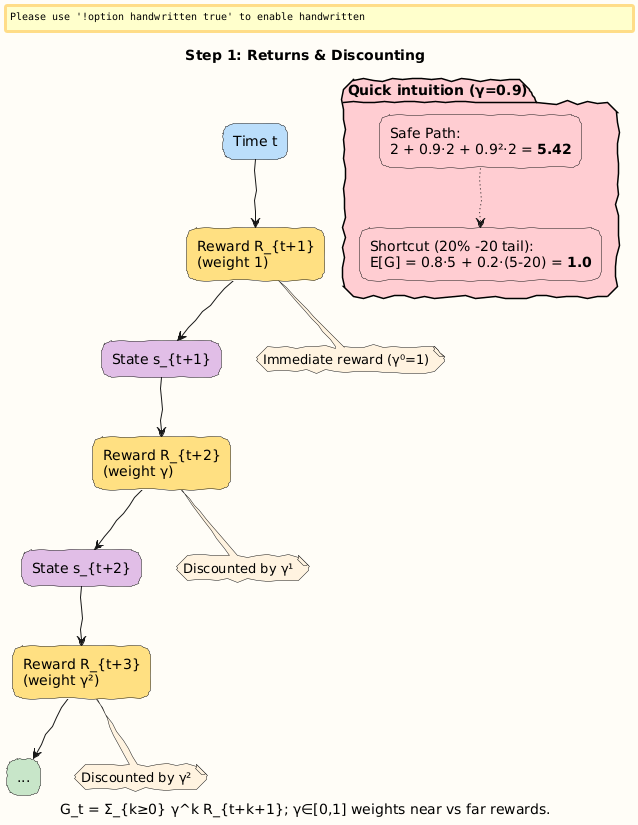
Step 1. The Return: Summing the Future
Formally, the return from time step t is:
Where:
R_{t+k+1}is the reward received k steps into the future.γ∈ [0, 1] is the discount factor, controlling how much the agent cares about the future.
Interpretation:
γ= 0 → live in the moment (myopic).γ= 1 → care equally about all future rewards.
Numerical Example 1: A Shortcut vs Safe Path
Suppose an agent (a delivery robot) has two paths:
Shortcut: Rewards = [+5 now, then +0, but with 20% chance of -20 in the next step].
Safe Path: Rewards = [+2, +2, +2, always].
Let γ = 0.9.
Safe Path Return:
Shortcut Expected Return:
Interpretation: Although the shortcut looks tempting (big +5 upfront), the discounted expectation makes it worse than the safe path (1 < 5.42).
Visual:
Step 2. Value Functions: Predicting the Future
Instead of recalculating full returns each time, the agent builds functions:
State value:
Action value:
Intuition:
V^\pi(s): “How good is it to be in statesif I keep following my policy?”Q^\pi(s, a): “How good is it to take actionain states, then follow my policy?”
These compress the entire future tree into single numbers, powerful abstractions for planning.
Numerical Example 2: Gridworld Step
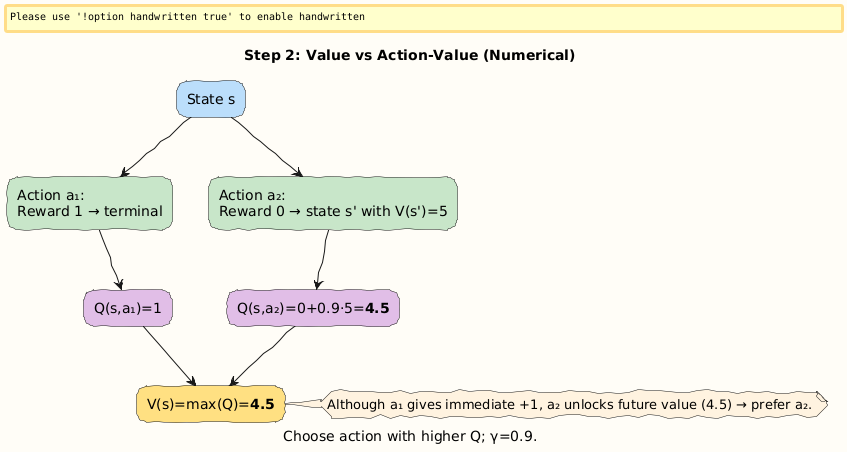
Suppose an agent in state s has two possible actions:
Action
a_1: Reward = +1, moves to terminal state.Action
a_2: Reward = 0, but leads to another state worthV(s’)= 5.
With γ = 0.9:
So:
Interpretation: Even though action a_1 gives immediate satisfaction (+1), the agent learns to prefer a_2, which unlocks a much better future (worth 4.5).
Visual:
Step 3. Bellman Recursion: The Self-Referential Genius
The Bellman equation expresses this recursive reasoning:
For value functions:
For optimal value functions:
Interpretation:
The value of today depends on reward now + discounted value of tomorrow.
Like a recursive definition of “goodness”.
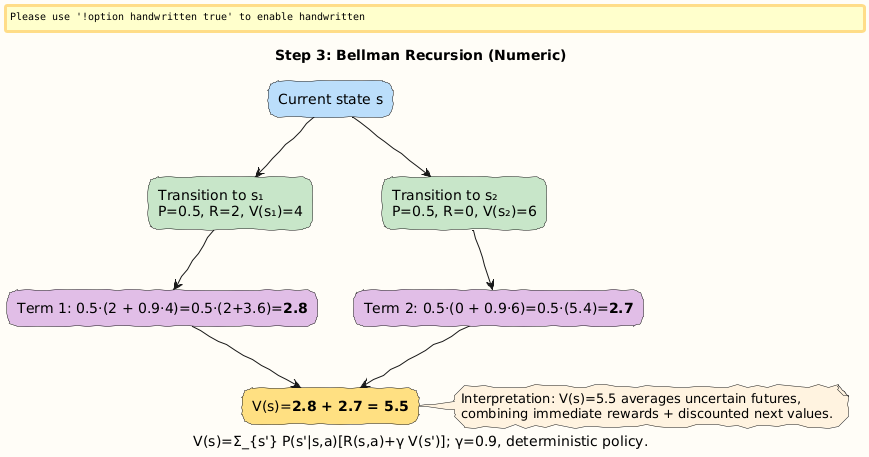
Numerical Example 3: Bellman Update
Consider a simple MDP with:
State
s.Two possible next states:
s_1: reward = 2, probability = 0.5,V(s_1)= 4.s_2: reward = 0, probability = 0.5,V(s_2)= 6.Discount factor:
γ= 0.9.Policy: deterministic (always takes action aaa).
Using Bellman equation:
Interpretation: The agent assigns state sss a value of 5.5, because it averages over uncertain futures, weighting rewards and next-state values.
Visual:
Importance of it: From Chess to Driving
In chess, the “value” of a board position is not just the current material but the promised outcomes from good play.
In self-driving cars, the “value” of being at an intersection is not only safety now but the probability of reaching the destination.
This recursive planning is the heart of RL.
Special: Learn More in Learning to Learn: Reinforcement Learning Explained for Humans
If today’s math feels like both beautiful and slightly overwhelming, that’s exactly why I wrote my book:
Learning to Learn: Reinforcement Learning Explained for Humans
It takes you step by step, from everyday analogies (like the biking shortcut problem above) to rigorous mathematics, all while keeping the storytelling alive.
Grab it here:
Closing
We started with returns: how agents add up futures.
We built value functions: compressing expectations into numbers.
We introduced the Bellman recursion: the mathematical law that forces agents to think about tomorrow today, with a worked example that shows exactly how an agent averages over uncertain futures.
Next time: we dive into the eternal dilemma, Exploration vs Exploitation.
Follow and Share
You can follow me on Medium to read more: https://medium.com/@satyamcser
#ReinforcementLearning #MachineLearning #BellmanEquation #ValueFunctions #Discounting #Gridworld #AIExplained #MLForHumans #RLMath #satmis