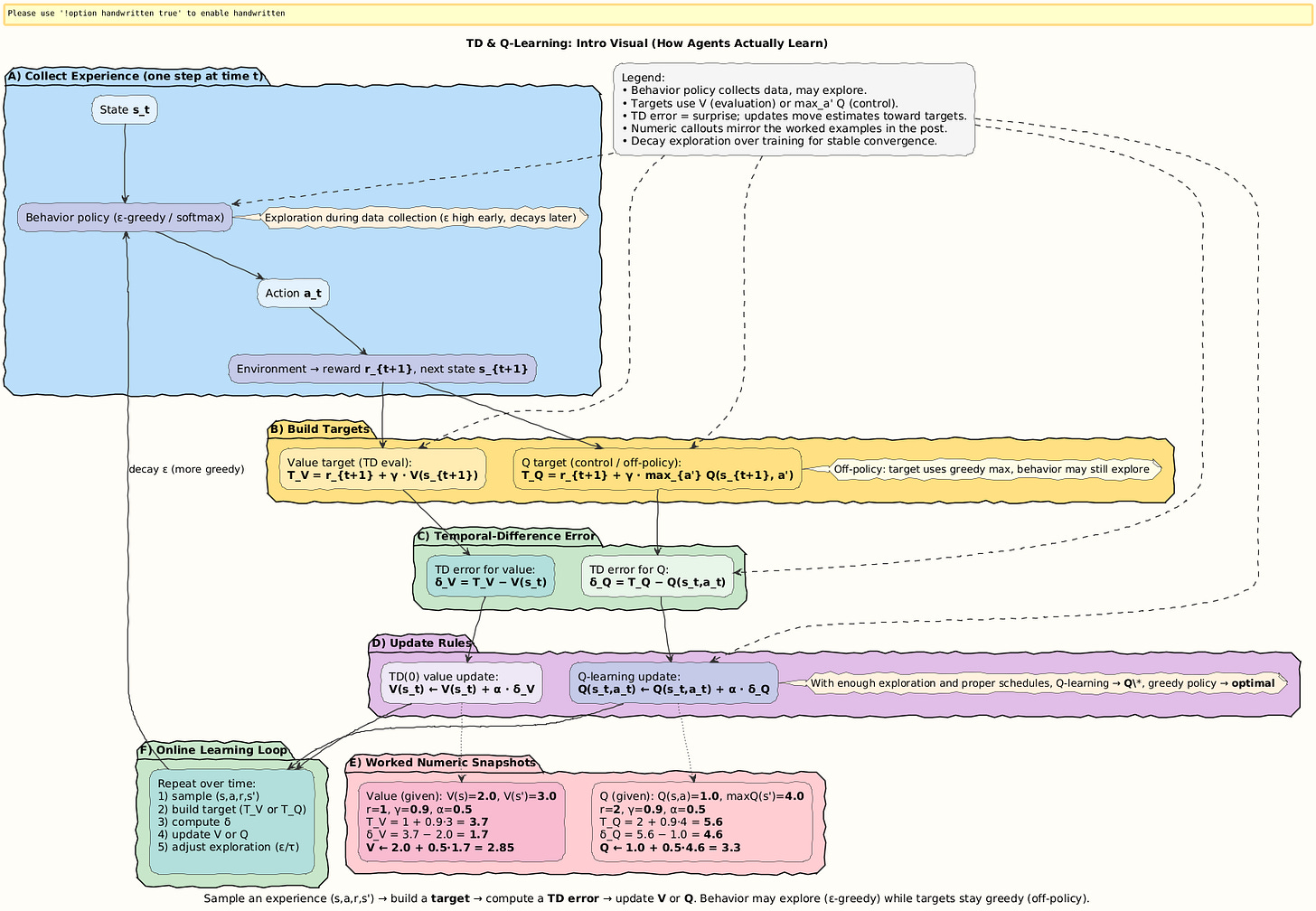
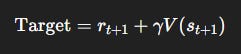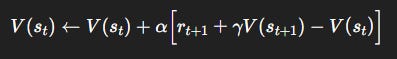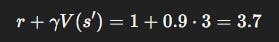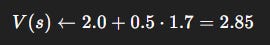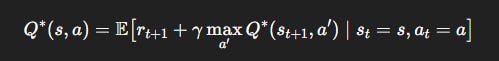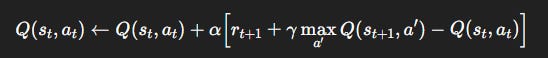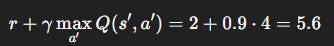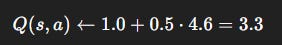Q-Learning and Temporal Difference Learning: How Agents Actually Learn
The Story: Learning by Doing
Imagine a child learning to ride a bicycle. No one gives them the full physics equations of balance and motion. Instead, they try, wobble, sometimes fall, and adjust based on experience.
This is exactly how RL agents learn: not by knowing the full world model, but by interacting with it.
Dynamic Programming assumes we know transition probabilities
P(s′ ∣ s, a).In the real world, that’s impossible.
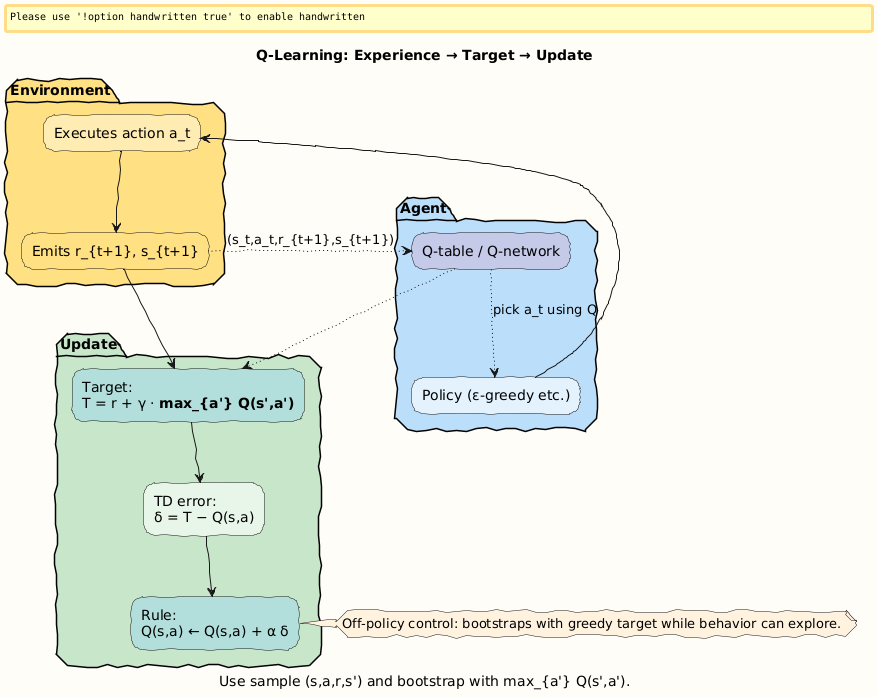
Temporal Difference (TD) Learning and Q-Learning are the methods that let agents learn directly from sampled experience.
They are the bridge between theory (Bellman equations) and practice (learning online from data).
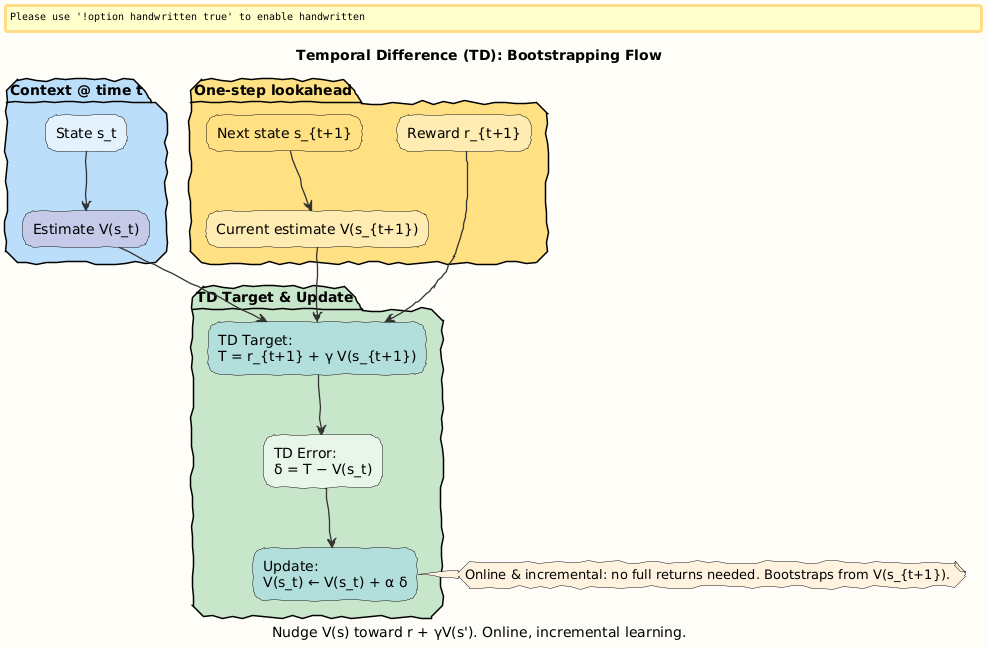
Step 1. Bootstrapping: Learning from Partial Futures
The central trick is bootstrapping: instead of waiting until the very end of an episode to compute the full return G_t, TD methods update value estimates using:
That is, the value of the current state is nudged toward the immediate reward plus the discounted estimate of the next state’s value.
This makes TD updates online and incremental.
Visual:
Step 2. TD(0) Update Rule
The simplest TD method is TD(0):
α: learning rate (0 <α≤ 1).Bracketed term = TD error:
Interpretation: Adjust the old value estimate by a fraction α of the surprise (prediction error).
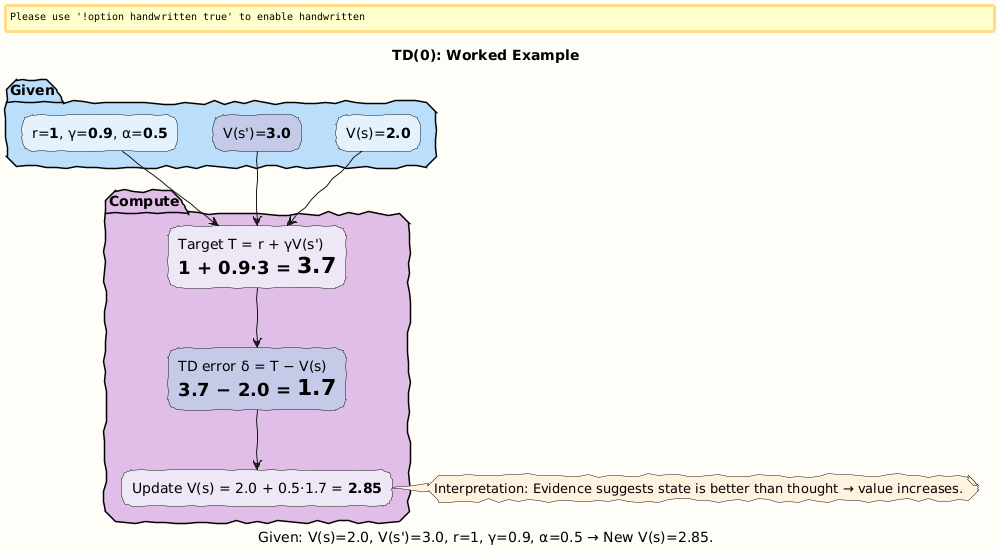
Numerical Example 1: TD State Update
Suppose:
Current estimate:
V(s)= 2.0.Next state’s value:
V(s’)= 3.0.Reward:
r= 1.Parameters:
γ= 0.9,α= 0.5.
Step 1: Compute target
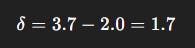
Step 2: Compute TD error
Step 3: Update
Interpretation: The agent thought the state was worth 2.0, but experience suggests it’s closer to 3.7. After the update, it moves halfway there (2.85). Over many updates, values converge.
Visual:
Step 3. From Values to Q-Values
Instead of just evaluating states, agents often need to evaluate state-action pairs.
The optimal Q-function satisfies the Bellman optimality equation:
TD learning turns this into an update rule:
This is Q-learning:
Uses real experience.
Bootstraps with the max operator.
Converges to Q* under conditions.
Visual:
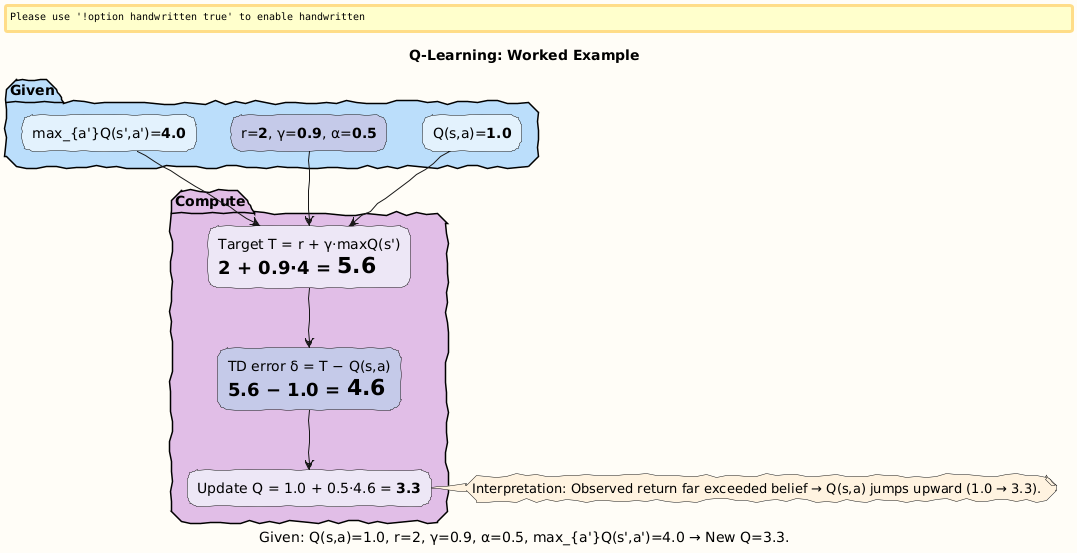
Numerical Example 2: Q-Learning Update
Suppose:
Current state:
s.Action a chosen.
Reward received:
r= 2.Discount
γ= 0.9, learning rateα= 0.5.Current Q-value:
Q(s, a)= 1.0.Next state’s best action value:
max_{a’} Q(s’, a’)= 4.0.
Step 1: Compute target
Step 2: Compute TD error
Step 3: Update
Interpretation: The agent drastically increases its estimate of action a’s value, from 1.0 → 3.3, because the observed return was far higher than expected. With more updates, Q-values converge toward the optimal policy.
Visual:
Step 4. Why TD and Q-Learning Matter
No model needed: Learn directly from raw experience.
Efficient: Update online instead of waiting for full episodes.
Bootstrapping: Use estimates to improve themselves.
Foundation: Modern Deep RL (DQN, Actor–Critic) is built on these principles.
Analogy: You don’t need to play every possible chess game. If you see one line leads to disaster, you immediately adjust your value of that move.
Special: Learn More in Learning to Learn: Reinforcement Learning Explained for Humans
If this post clicked, and you want to master TD learning step-by-step, with more examples, derivations, and even code, check out my book:
Learning to Learn: Reinforcement Learning Explained for Humans
It covers:
TD learning explained with analogies and math.
Worked problems like the ones we solved above.
Code snippets to implement TD(0) and Q-learning.
Bridges from classical tabular RL to deep RL.
Grab it here:
Closing
We introduced TD learning: incremental updates from experience.
We extended to Q-learning, the most widely used value-based method.
We worked through two detailed numerical examples:
TD state update (2.0 → 2.85).
Q-learning update (1.0 → 3.3).
We saw why TD methods are the engine that powers practical RL.
Next post → Policy Gradients & Actor–Critic, where we move from value-based to policy-based learning.
Follow and Share
You can follow me on Medium to read more: https://medium.com/@satyamcser
#ReinforcementLearning #TemporalDifference #QLearning #MachineLearning #BellmanEquation #TDLearning #Bootstrapping #RLMath #AIExplained #DeepRL #satmis