Kolmogorov–Sinai Entropy in Language Modeling – Measuring Predictive Complexity in Neural Text Generators
A dynamical systems perspective on uncertainty, memory, and model behavior.
Modern language models are extraordinary at predicting the next token. But what if we asked:
How predictable are the predictions themselves?
Instead of relying solely on perplexity or loss, we turn to a powerful mathematical concept from ergodic theory and dynamical systems:
> Kolmogorov–Sinai (KS) Entropy – the rate at which new information is generated in a system.
In deep learning, this allows us to go beyond accuracy and ask:
How complex is the internal model of a sequence?
How much structure is it exploiting or memorizing?
Where does uncertainty actually emerge?
---
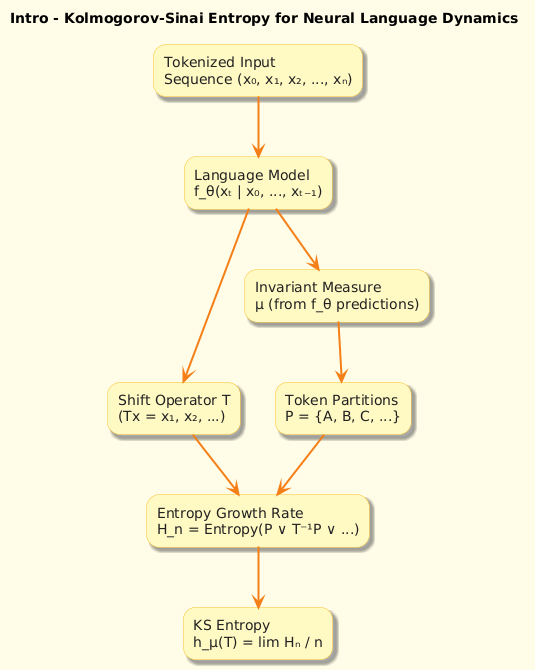
1️⃣ What is Kolmogorov–Sinai Entropy?
KS entropy originates from dynamical systems theory and is used to measure chaotic complexity.
It describes the average amount of new information per time step in a system’s evolution:
h_{\mu}(T) = \sup_{\mathcal{P}} \lim_{n \to \infty} \frac{1}{n} H_{\mu}\left( \bigvee_{i=0}^{n-1} T^{-i}\mathcal{P} \right)
T : the evolution map (like the shift operator on a sequence)
\mu : invariant measure (like a model’s learned distribution)
P : a partition of the space (e.g., vocabulary tokens)
Intuition:
KS entropy captures how fast uncertainty grows when observing a sequence of predictions. It quantifies how many bits per step are irreducibly new.
---
2️⃣ From Dynamical Systems to Language Models
In autoregressive language models:
The text generation process is a dynamical system
The shift operator moves through the token stream
The model’s distribution over next tokens creates a stochastic process
We interpret:
A model with low KS entropy as highly confident and possibly overfitting
A model with high KS entropy as chaotic, poorly structured, or uncertain
An ideal model balances predictive complexity with generalization
---
3️⃣ Why KS Entropy Matters in LLMs
a. Beyond Perplexity
Perplexity only measures cross-entropy of next-token prediction. It doesn’t:
Capture long-term structure
Reflect internal model state transitions
Quantify token-to-token dependency complexity
KS entropy does.
---
b. Memory Length and Uncertainty
A model that uses longer context to reduce uncertainty will have:
A lower KS entropy after sufficient history
A sharp entropy drop if it memorizes known sequences
A gradual decay for highly structured, natural language
This allows us to map entropy flow across sequence positions.
---
c. Overfitting Detection
A model that overfits (e.g., repeats training data verbatim) will show:
Low KS entropy but high information concentration
Sharp entropy valleys at seen substrings
Flat entropy elsewhere
This entropy profile acts like a diagnostic heatmap.
---
d. Scaling and Capacity Laws
As model size increases:
KS entropy tends to decrease for structured datasets
But may increase for noisy or ambiguous corpora
This gives a thermodynamic lens on scaling laws—how much additional entropy is managed by bigger models.
---
e. Sampling and Creativity
Models tuned for creativity or diversity may be designed to:
Increase KS entropy in controlled ways
Maintain uncertainty beyond the next token
Encourage chaotic continuations in open-ended tasks
---
4️⃣ Applications in Modern Language Modeling
Entropy Maps – visualize KS entropy across token positions
Context Length Benchmarking – evaluate how entropy decays with history
Architectural Diagnostics – compare models via their entropy structure
Entropy-Regularized Decoding – add constraints to retain exploration
---
Visual Insights Coming Up
1. Intro Visual – Sequence → Shift → KS Entropy
2. KS Entropy Pipeline – Model → Partitions → Entropy Rate
3. Entropy Map of Token Stream – Visualization of uncertainty
4. Entropy & Scaling – Capacity vs complexity
5. Model Fingerprinting by KS Curve – Comparing internal chaos
---
Final Thoughts
KS entropy gives us a spectral lens on model behavior.
While perplexity tells us “how wrong” a model is,
KS entropy tells us how uncertain the model's world is—and how much it invents, forgets, or learns with each step.
It’s the difference between:
Measuring an answer
And measuring the system that answers.
#KolmogorovSinaiEntropy #LanguageModeling #EntropyInAI #DynamicalSystems #LLMComplexity #ModelUncertainty #satmis