Kolmogorov Complexity Meets Prompt Design – The Minimal Description Principle in Language Models
From compressed strings to compressed thought—why the shortest prompt often wins.
In the age of Large Language Models (LLMs), prompt design is an art.
But it can also be a science.
One of the most powerful and underused tools to analyze prompt effectiveness is a concept from algorithmic information theory:
Kolmogorov Complexity.
It tells us that the best way to describe something is often the shortest program that generates it.
This idea lies at the heart of compression, learning, and even creativity—and now, it’s shaping how we interact with LLMs.
---
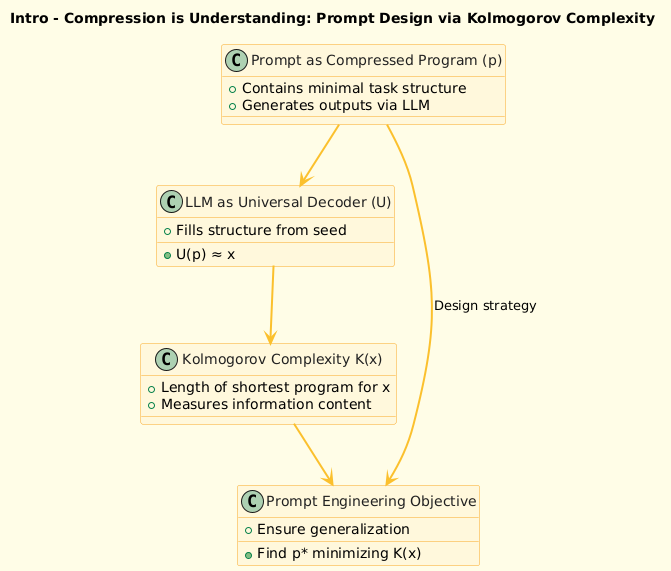
1️⃣ What is Kolmogorov Complexity?
Definition:
The Kolmogorov Complexity K(x) of a string x is the length of the shortest program (in some fixed language) that outputs x.
Mathematically:
K(x) = \min \{ |p| : U(p) = x \}
U is a universal Turing machine
|p| is the length of the program
It’s a measure of incompressibility:
If x has a short program → it’s structured
If no shorter program than x itself → it’s random
Kolmogorov complexity is non-computable, but it serves as a theoretical gold standard for evaluating simplicity and structure.
---
2️⃣ Why It Matters for Prompt Design
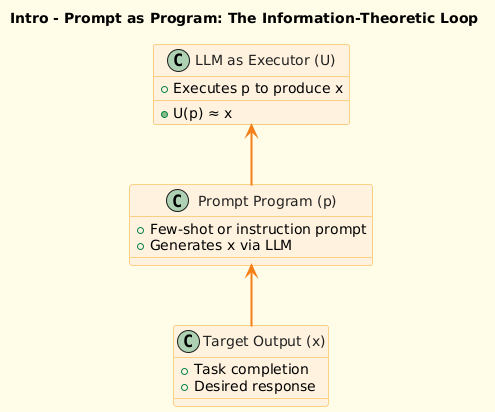
When designing prompts for LLMs, we’re essentially asking:
> What is the minimum information required to elicit the desired response?
Kolmogorov complexity gives a powerful lens:
Shorter prompts = lower complexity = stronger priors
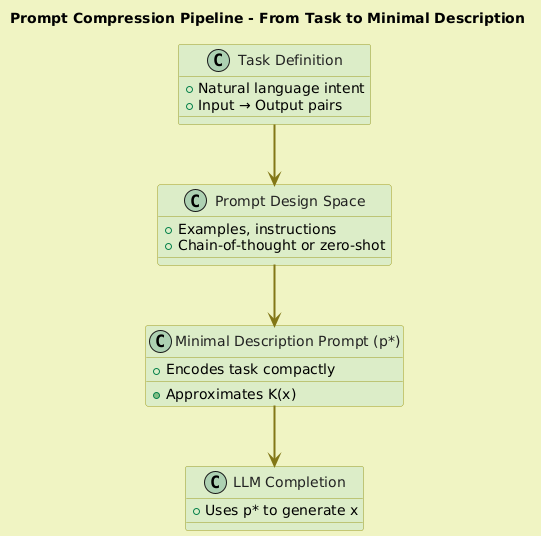
Good prompts compress task structure into minimal examples
LLMs behave like pattern-completion machines—they work better with low-complexity seeds
---
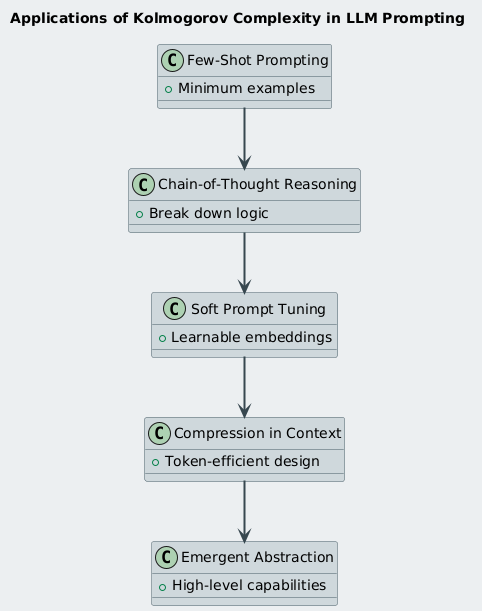
3️⃣ Core Applications in LLMs
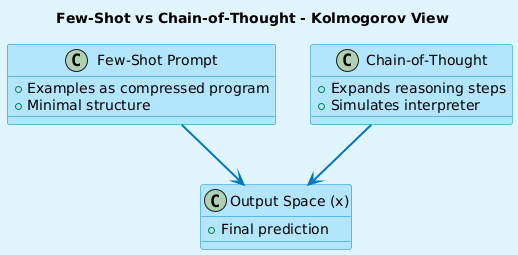
a. Few-Shot Prompting
Given 2–3 examples, we hope the model generalizes the pattern.
Better prompts are those that minimally encode the pattern
The few examples act as a compressed program that reconstructs the full distribution
In essence, the prompt approximates the program such that:
\text{LLM}(p) \approx \text{Target task}
---
b. Chain-of-Thought (CoT) as Decompression
CoT prompting doesn’t always shorten the input—but it helps the model simulate a lower-complexity reasoning function.
Human-readable steps help the LLM build intermediate states
CoT = interpreter loop for a complex answer
This aligns with:
K(\text{output}) \leq K(\text{reasoning steps}) + K(\text{interpreter})
---
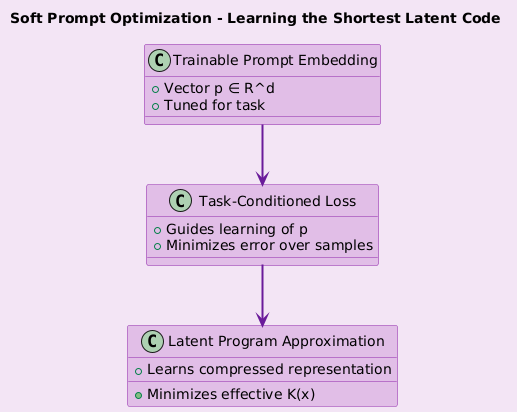
c. Prompt Tuning / Soft Prompts
Trainable prompts are vectors in embedding space.
Good soft prompts learn to:
Minimize task-specific Kolmogorov complexity
Capture structure in low-bit representations
Think of it as:
> Backpropagating into the compressed program.
---
d. Compression in Context Window
Tokens are expensive. LLMs perform better when the context contains:
High signal-to-noise ratio
Low-redundancy instructions
Predictable semantic patterns
Thus, the prompt’s effective complexity should be minimized—even if its token length isn’t.
---
e. Emergent Behaviors and Complexity Thresholds
LLMs often show emergent capabilities at scale (e.g., arithmetic, theory-of-mind).
These behaviors emerge when:
The training distribution allows for programs with compact descriptions
The model capacity allows execution of higher-complexity functions
Kolmogorov complexity provides a lens to ask:
> What capabilities are unlocked at each compression level?
---
4️⃣ What This Adds to Prompt Engineering
Instead of treating prompts as trial-and-error strings, we now see them as:
Programs that instruct the model
Compressed semantic functions
Descriptive priors for task generation
This enables:
Analytical prompt design based on structure
Compression-guided evaluation of prompts
Token-efficient task encoding
---
Visual Insights Coming Up
1. Intro Visual – Prompt as program: The information-theoretic loop
2. Prompt Compression Pipeline – From task to minimal description
3. Few-Shot vs Chain-of-Thought – Kolmogorov lens
4. Soft Prompt Optimization – Learning the shortest latent code
5. Application Graph – Where Kolmogorov complexity improves LLM usage
---
Final Thoughts
In a world of trillion-token models, the best prompts aren’t just long—they’re smart.
Kolmogorov Complexity shows us that simplicity isn’t triviality—it’s power.
Every prompt you write is a program. And the best programs are those that say more with less.
By thinking in terms of compression, structure, and minimal description, we elevate prompt engineering into a formal science—backed by the deep logic of information theory.
#KolmogorovComplexity #PromptDesign #LLMOptimization #InformationTheory #PromptEngineering #Compression #FewShotLearning #satmis