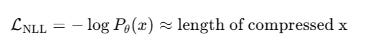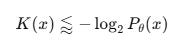How AI Models Compress the World: Kolmogorov Meets Transformers

What if your favorite transformer isn’t just predicting the next token… but actually learning to compress meaning itself?

---

---

Intro: Your Language Model is a Compressor

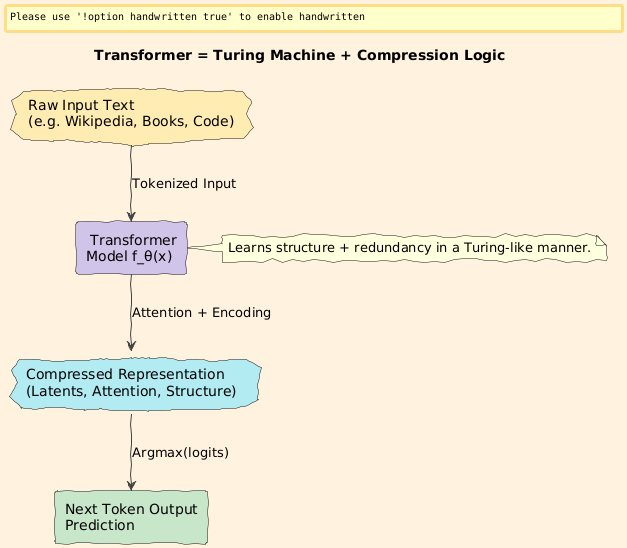
Transformers aren’t just memorizing patterns: they’re building compressed programs that best explain the sequences they see.

In the deepest sense, your model is learning to encode reality as succinctly as possible…
just like Kolmogorov complexity tried to do 60 years ago.

---

Visual: “Transformer as a Turing Machine that Compresses Data”

---

The Core Idea: Kolmogorov Complexity

Let’s say you have a string:

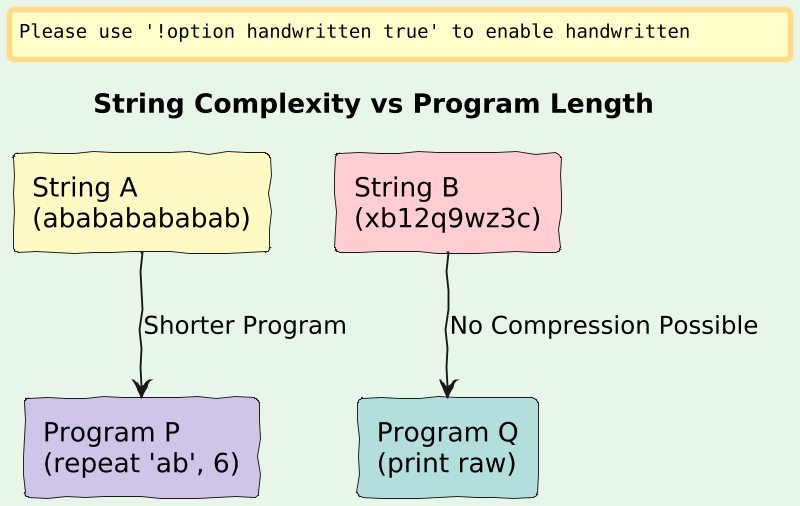
A = "abababababababababababababababab"

You could describe this string in two ways:

1. Naively:

Just store it as-is → 32 characters.

2. Programmatically:

“Repeat ‘ab’ 16 times” → Short Python program.

This second form is compression, and Kolmogorov complexity formalizes this:

Definition:
The Kolmogorov complexity K(x) of a string x is the length of the shortest program p such that:

U(p) = x

Where U is a fixed universal Turing machine.

The shorter the program, the simpler the object.
Random strings (like "xb1a8qz...") have no shorter description than themselves → high complexity.

---

Visual: “Program Length vs String Length: Visualizing K(x)”

---

LLMs: From Compression to Prediction

Now imagine your LLM trying to predict:

The capital of France is ___

Behind the scenes, it is:

• Compressing the distribution over all sentences it has ever seen,

• Using patterns to reduce redundancy (like “Paris” often follows “capital of France”),

• Producing the shortest latent encoding that still reconstructs the sequence.

In fact, many LLM training objectives are implicitly minimizing a description length:

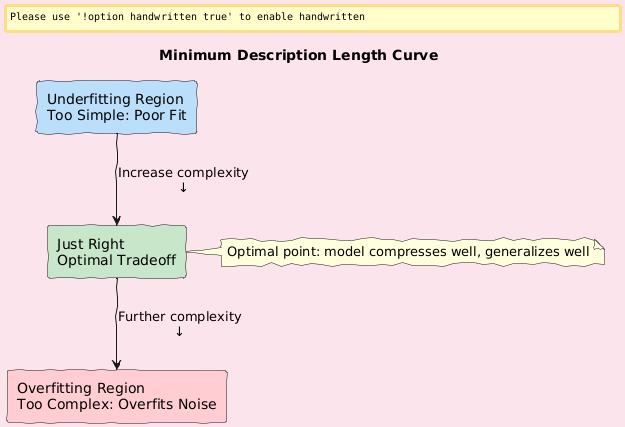
This connects to the Minimum Description Length (MDL) principle:

The best model is the one that compresses the data the most.

---

Visual: “MDL Curve: Model Complexity vs Log-Likelihood”

---

Transformers Approximate Kolmogorov Complexity

Let’s go further.

A transformer is a parametric function f_θ(x) that:

• Encodes sequences with limited context (attention)

• Learns structural biases about the world (grammar, logic, causality)

• Produces next-token predictions that effectively model P(x) — the compressed prior over all language

It’s like a giant approximation of the true K(x):

So every time a transformer makes a prediction, it’s trying to minimize the length of the surprise.

---

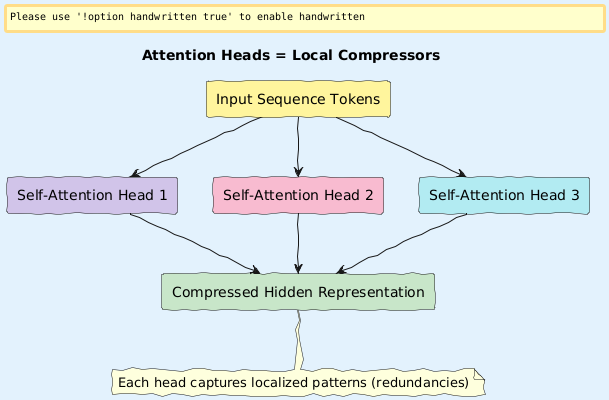
Visual: “Transformer Attention Heads as Local Compressors”

---

Compression, Generalization, and Emergence

Why does this matter?

Because:

• Generalization = good compression

• Models that generalize well are the ones that assign high probability to test samples, meaning they compress them too.

This also explains emergent abilities:

At scale, transformers compress broader and deeper distributions ,  giving rise to new capabilities.

---

Visual: “Scaling Law vs Compression Ratio: Phase Transition of Capabilities”

---

Satyam’s Explanation:

Imagine trying to write a story using the fewest words possible, but it should still mean the same thing.

Your model is doing the same:
It finds clever shortcuts (like patterns and templates) to retell the world in shorter and shorter ways.

That’s why it can answer your questions:
It already stored a compressed version of the answers!

---

Technical Summary

---

Q1/A★ Research Framing

Problem

Understanding what enables generalization and abstraction in large-scale language models. Why do they work so well on unseen data?

Solution

Frame transformers as compression machines approximating Kolmogorov complexity via learned priors and next-token entropy minimization.

Novelty

• Unifies information theory, algorithmic complexity, and transformer learning dynamics

• Bridges Bayesian compression and emergent behavior

Contribution

• Proposes a new lens to interpret attention heads as local compressors

• Suggests entropy compression metrics to track semantic abstraction quality

Why Q1/A★ Level

This topic connects fundamental theory (MDL, K-complexity) with current LLM performance: touching core open questions in generalization, scalability, and emergence, suitable for top-tier venues like ICLR, NeurIPS, or Information Sciences.

---

Final Thought

So the next time your transformer spits out a fluent sentence, remember:

it’s not just predicting the next word…
it’s compressing the universe to fit in 128 hidden dimensions.

---

Follow and Share

You can follow me on Medium to read more: https://medium.com/@satyamcser

---

#KolmogorovComplexity #Transformers #Compression #LLM #MDL #Generalization #DeepLearningTheory #satmis

---